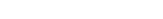凸优化综述(上)_琳琅-琳琅娱乐餐具销售公司

新闻中心

全国服务热线：0898-08980898
地址：江西省南昌市
邮编：000000
电话：0898-08980898
传真：400-123456

公司新闻

凸优化综述(上)

发布时间：2024-05-06 05:22:54 浏览：次

本篇为课程CS229的补充材料Convex Optimization Overview^[1]的笔记。许多机器学习方法如最小二乘法、logistic回归、支持向量机都可以归纳到凸优化问题的框架之下，并得到有效的解决。这篇文章主要对原凸优化讲义内容进行总结，并对部分定义证明进行适当的补充。下半部分为凸优化综述(下)

先验知识
凸集(Convex Sets)
凸函数
凸性的一阶条件(First Order Condition for Convexity)
凸性的二阶条件(Second Order Condition for Convexity)
Sublevel Sets
凸函数的例子
凸优化问题中的全局最优值

范数

非正式地说，向量 $x$ 的范数 $\\|x\\|$ 是这个向量的长度的度量，以第二范数欧几里得范数为例， $\\|x\\|_{2}=\\sqrt{\\sum_{i=1}^{n}x_{i}^{2}}$ ，写成向量形式为 $\\|x\\|_{2}^{2}=x^{T}x$ 。更正式地说，范数是满足以下四个条件的任何函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ ：

非负性：对于所有 $x \\in \\mathbb{R}^{n}$ ，有 $f(x)\\geq0$
正定性：当且仅当 $x=0$ 的时候 $f(x)=0$
齐次性：对于所有 $x \\in \\mathbb{R}^{n}, t \\in \\mathbb{R}$ ， $f(t x)=|t| f(x)$
三角不等式：对于所有 $x, y \\in \\mathbb{R}^{n}$ ， $f(x+y) \\leq f(x)+f(y)$

仿射子空间、多面体、仿射变换以及仿射函数

定义表述如下：

仿射子空间(affine subspaces)：给定矩阵 $A \\in \\mathbb{R}^{m \ imes n}$ 以及向量 $b \\in \\mathbb{R}^{m}$ ，仿射子空间为集合 $\\left\\{x \\in \\mathbb{R}^{n}: A x=b\\right\\}$
多面体(polyhedra)：类似的，多面体为集合 $\\left\\{x \\in \\mathbb{R}^{n}: A x \\preceq b\\right\\}$ ；注意，此处的符号 $\\preceq$ 表示逐元素不等，即 $Ax$ 的结果所有位置上的值都小于向量 $b$ 对应位置上的值
仿射变换(affine transformation)：从 $\\mathbb R^n$ 到 $\\mathbb R^m$ 的变换 $y=Ax+c$ 被称为仿射变换，其中 $y \\in \\mathbb{R}^{m}$ ， $A \\in \\mathbb{R}^{m \ imes n}$ ， $c \\in \\mathbb{R}^{m}$ 为常向量
仿射函数(affine function)：仿射函数为仿射变换的一种特殊情况，当仿射变换中的 $m=1$ 时， $A^T \\in \\mathbb{R}^ n$ ， $y,c$ 都为常数；此外，如果将此处 $y=Ax+c$ 中的截距 $c$ 去掉，剩下的部分 $y=Ax$ 被称为线性函数

二次函数的 $Hessian$ 矩阵

设二次函数 $f(x)=x^{T}A x$ ，其中矩阵 $A$ 为对称矩阵 $A \\in \\mathbb{S}^{n}$ 。 $f(x)$ 可以进行如下展开： $f(x)=\\sum_{i=1}^{n}\\sum_{j=1}^{n}A_{i j}x_{i}x_{j}\\\\$ 先对 $f(x)$ 求导，以 $x_k$ 项为例： $\\begin{aligned}\\frac{\\partial f(x)}{\\partial x_{k}}&=\\frac{\\partial}{\\partial x_{k}}\\sum_{i=1}^{n}\\sum_{j=1}^{n}A_{i j}x_{i}x_{j}\\\\ &=\\frac{\\partial}{\\partial x_{k}}\\left[\\sum_{i \ eq k}\\sum_{j \ eq k}A_{i j}x_{i}x_{j}+\\sum_{i \ eq k}A_{i k}x_{i}x_{k}+\\sum_{j \ eq k}A_{k j}x_{k}x_{j}+A_{k k}x_{k}^{2}\\right]\\\\ &=\\sum_{i \ eq k}A_{i k}x_{i}+\\sum_{j \ eq k}A_{k j}x_{j}+2 A_{k k}x_{k}\\\\ &=\\sum_{i=1}^{n}A_{i k}x_{i}+\\sum_{j=1}^{n}A_{k j}x_{j}=2 \\sum_{i=1}^{n}A_{k i}x_{i}\\end{aligned}\\\\$ 由此可以推出，对于整体而言 $\ abla_{x}x^{T}A x=2 A x\\\\$ 再求 $f(x)$ 的 $Hessian$ 矩阵： $\\frac{\\partial^{2}f(x)}{\\partial x_{k}\\partial x_{\\ell}}=\\frac{\\partial}{\\partial x_{k}}\\left[\\frac{\\partial f(x)}{\\partial x_{\\ell}}\\right]=\\frac{\\partial}{\\partial x_{k}}\\left[2 \\sum_{i=1}^{n}A_{\\ell i}x_{i}\\right]=2 A_{\\ell k}=2 A_{k \\ell}\\\\$ 由此可以推出，对于整体而言 $\ abla_{x}^{2}x^{T}A x=2 A\\\\$ 为了方便记忆这些结论，可以将上述结论与单变量求导的情况进行类比，例如将 $\ abla_{x}x^{T}A x=2 A x$ 类比为 $\\frac{\\partial ax^2}{\\partial x}=2ax$ ，将 $\ abla_{x}^{2}x^{T}A x=2 A$ 类比为 $\\frac{\\partial ax^2}{\\partial x^2}=2a$

矩阵求导总结：

$\ abla_{x}b^{T}x=b$
$\ abla_{x}x^{T}A x=2 A x$
$\ abla_{x}^{2}x^{T}A x=2 A$

定义：对于任何 $x,y\\in C$ ， $\ heta \\in \\mathbb R$ 且 $0 \\leq \ heta \\leq 1$ ，若 $\ heta x+(1-\ heta) y \\in C$ 成立，则称集合 $C$ 为凸的。

可以通过下面的图来直观地理解什么是凸集：对于凸集 $C$ 中的任意两个元素 $x,y$ ，用一条线段将这两个元素连起来，那么这条线段上的每个元素都属于 $C$ 。

典型的凸集有：

实数向量 $\\mathbb R^n$
非负象限
范数球 $\\{x :\\|x\\| \\leq 1\\}$ ：设存在 $x, y \\in \\mathbb{R}^{n}$ ， $\\|x\\| \\leq 1$ ， $\\|y\\| \\leq 1$ ，且 $0 \\leq \ heta \\leq 1$ ，利用范数的齐次性以及三角不等式有 $\\|\ heta x+(1-\ heta) y\\| \\leq\\|\ heta x\\|+\\|(1-\ heta) y\\|=\ heta\\|x\\|+(1-\ heta)\\|y\\|\\leq1$
仿射子空间
多面体
凸集的交集：设集合 $C_{1}, C_{2}, \\ldots, C_{k}$ 为凸集，那么它们的交集 $\\bigcap_{i=1}^{k}C_{i}=\\left\\{x : x \\in C_{i}\\quad \\forall i=1, \\ldots, k\\right\\}\\\\$ 也是凸集。需要注意，凸集的并集往往不是凸集
半正定矩阵：设存在两个半正定矩阵 $A, B \\in \\mathbb{S}_{+}^{n}$ ， $0 \\leq \ heta \\leq 1$ ，对于所有的 $x \\in \\mathbb{R}^{n}$ 有 $x^{T}(\ heta A+(1-\ heta) B) x\\\\$ $=\ heta x^{T}A x+(1-\ heta) x^{T}B x\\\\$ 而其中 $x^{T}A x \\geq0$ ， $x^{T}B x\\geq0$ ，所以 $x^{T}(\ heta A+(1-\ heta) B) x\\geq0\\\\$ 所以半正定矩阵也是凸集

证明集合属于凸集的关键在于明确原集合的定义，之后利用凸集的定义进行证明即可。

定义：对于函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ ，如果它的域 $\\mathcal{D}(f)$ 是一个凸集，并且对于所有 $x,y\\in \\mathcal{D}(f)$ ， $\ heta \\in \\mathbb R,0 \\leq \ heta \\leq 1$ ，有 $f(\ heta x+(1-\ heta) y) \\leq \ heta f(x)+(1-\ heta) f(y)\\\\$ 那么函数 $f$ 被称为凸函数。

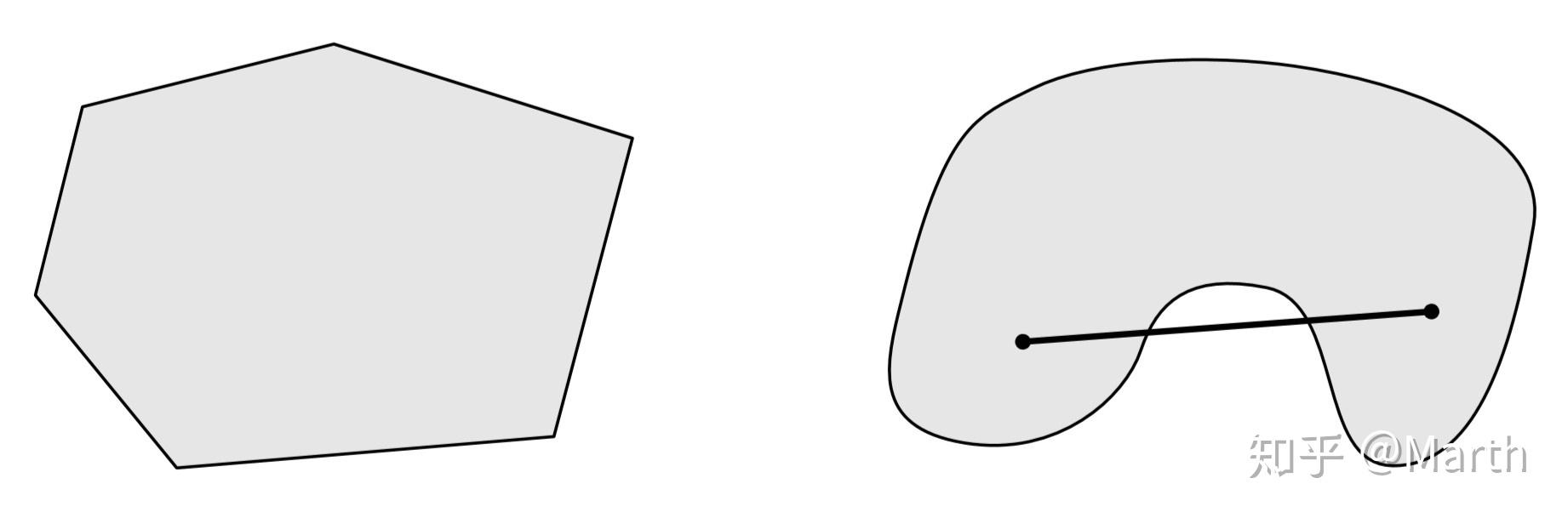
可以通过下面的图来直观地理解什么是凸函数：如果取凸函数上的两点并在它们之间连一条线段，那么两点之间的函数部分都会在这条线段之下。

进一步定义，如果上述定义对 $x \ eq y$ 且 $0<\ heta<1$ 的条件成立，则称函数 $f$ 为严格凸函数。如果函数 $-f$ 为凸的，则定义 $f$ 为凹的，严格凹函数的定义以此类推。

定义：假设函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ 可微（即对于所有 $x\\in \\mathcal{D}(f)$ ，导数 $\ abla_{x}f(x)$ 恒存在），当且仅当 $\\mathcal{D}(f)$ 为凸集且对于所有 $x,y\\in \\mathcal{D}(f)$ $f(y) \\geq f(x)+\ abla_{x}f(x)^{T}(y-x)\\\\$ 都成立的时候，可以称函数 $f$ 是凸函数。

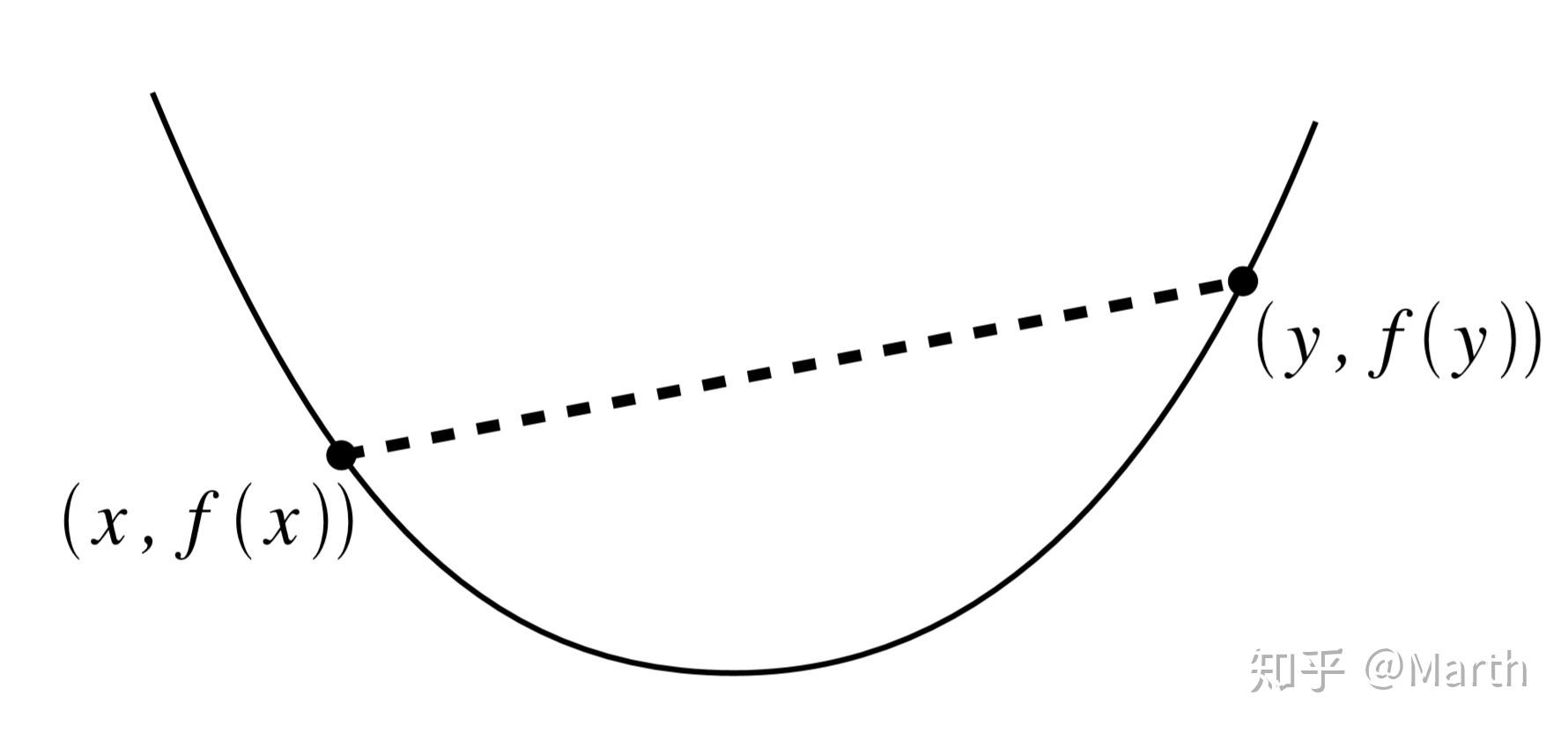
可以通过下面的图来直观地理解什么是凸性的一阶条件：对于凸函数上的任一点 $x$ ，它所在处的切平面永远在函数 $f$ 下方。

凸性的一阶条件可以由凸函数的定义推导得到。凸函数的定义为（此处为了方便证明对变量 $x,y$ 的顺序做了些许改动）： $f(\ heta y+(1-\ heta) x) \\leq \ heta f(y)+(1-\ heta) f(x)\\\\$ 对这个式子的左边进行变换： $f(\ heta x+(1-\ heta) y)=f(y+ \ heta(x-y))$ ，再根据凸函数的定义有： $f(x+ \ heta(y-x))\\leq f(x)+ \ heta \\left(f(y)-f(x)\\right)\\\\$ 继续变换有： $f(x+ \ heta(y-x))- f(x)\\leq\ heta \\left(f(y)-f(x)\\right)\\\\$ $\\frac{f(x+ \ heta(y-x))- f(x)}{\ heta}\\leq f(y)-f(x)\\\\$ $\\frac{f(x+ \ heta(y-x))- f(x)}{\ heta}+f(x)\\leq f(y)\\\\$ 令 $g(\ heta)=f(x+ \ heta(y-x))$ ，易知 $f(x)=g(0)$ ，所以原式继续化简为： $f(y)\\geq\\frac{g(\ heta)-g(0)}{\ heta}+f(x)\\\\$ 当 $\ heta\\rightarrow 0$ 的时候， $\\frac{g(\ heta)-g(0)}{\ heta}$ 就等价于求 $g(\ heta)$ 在 $0$ 处的导数。而函数 $g(\ heta)$ 等同于函数 $f(X)$ 与函数 $X=x+\ heta(y-x)$ 的复合函数，因此 $\\frac{\\partial g}{\\partial \ heta}=\\frac{\\partial f}{\\partial X}\\frac{\\partial X}{\\partial \ heta}\\\\$ $=(y-x)\\frac{\\partial f}{\\partial X}\\\\$ 而 $\ heta\\rightarrow 0$ ， $X\\rightarrow x$ ，因此 $\\frac{\\partial g}{\\partial \ heta}=(y-x)\ abla_{x}f(x)\\\\$ 所以 $f(y)\\geq f(x)+(y-x)\ abla_{x}f(x)\\\\$ 即 $f(y)\\geq f(x)+\ abla_{x}f(x)^{T}(y-x)\\\\$

定义：假设函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ 是二阶可微的（对于所有 $x\\in \\mathcal{D}(f)$ ， $Hessian$ 矩阵都存在定义），当且仅当 $\\mathcal{D}(f)$ 为凸集且对于所有 $x\\in \\mathcal{D}(f)$ ，都有 $\ abla_{x}^{2}f(x) \\succeq 0$ 时，可以称函数 $f$ 是凸函数。

需要注意的是，此处的符号 $\\succeq$ 与上文多面体定义中用到的符号含义不同，此处的 $\\succeq$ 表示半正定，而非逐元素不等。

实际上，凸性的一阶条件和二阶条件是等价的，由凸性的一阶条件可以推出凸性的二阶条件。先写出函数 $f$ 在 $x$ 处的二阶泰勒展开： $f({X})=f\\left({x}\\right)+\ abla f\\left({x}\\right)\\left({X}-{x}\\right)+\\frac{1}{2}\\left({X}-{x}\\right)^{T}{H}\\left({X}-{x}\\right)+o\\left(\\left({X}-{x}\\right)^{T}\\left({X}-{x}\\right)\\right)\\\\$ 令 $\\Delta{x}={X}-{x}$ ，则有 $f({X})=f\\left({x}\\right)+\ abla f\\left({x}\\right) \\Delta{x}+\\frac{1}{2}\\Delta{x}^{T}{H}\\Delta{x}+o\\left(\\Delta{x}^{T}\\Delta{x}\\right)\\\\$ 此处式中的余项 $o\\left(\\Delta{x}^{T}\\Delta{x}\\right)$ 在 $\\|\\Delta{x}\\|\\rightarrow 0$ 时相对于 $\\|\\Delta{x}\\|$ 是更高阶的无穷小，所以当凸性的一阶条件 $f({X})\\geq f(x)+\ abla_{x}f(x)^{T}(X-x)$ 成立时，此处的二阶项 $\\frac{1}{2}\\Delta{x}^{T}{H}\\Delta{x}\\geq0$ 。其中， $H$ 为函数 $f$ 在点 $x$ 处的 $Hessian$ 矩阵， $\\frac{1}{2}\\Delta{x}^{T}{H}\\Delta{x}\\geq0$ 表示 $Hessian$ 矩阵为半正定。由 $Hessian$ 矩阵的定义 $\ abla_{x}^{2}f(x)\\in \\mathbb R^{n\ imes n}$ 可知，此时凸性的二阶条件 $\ abla_{x}^{2}f(x) \\succeq 0$ 成立。

为了便于理解，可以将输入变量 $x$ 设为一维的。此时凸性的二阶条件就等同于函数 $f$ 的二阶导数 $f^{\\prime \\prime}(x)\\geq0$ 。

更多关于凸函数的二阶条件以及 $Hessian$ 矩阵的讨论可以参考这个问题：怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的？

给定凸函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ 以及一个实数 $\\alpha \\in \\mathbb{R}$ ，集合 $\\alpha-sublevel$ $set$ 定义为： $\\{x \\in \\mathcal{D}(f) : f(x) \\leq \\alpha\\}\\\\$ 换句话说，对于函数 $f$ 来说， $\\alpha-sublevel$ $set$ 是所有符合条件 $f(x)\\leq \\alpha$ 的点的集合。 $\\alpha-sublevel$ $set$ 是个凸集，这一点可以利用定义进行证明。

指数函数
负对数函数
仿射函数：由于仿射函数项的最高次数为1，因此可知仿射函数的 $Hessian$ 矩阵 $\ abla_{x}^{2}f(x)=0$ （可以将 $Hessian$ 矩阵类比于函数的二阶导数），而由于零矩阵即是半正定的又是半负定的，所以仿射函数既是凸函数又是凹函数。实际上，仿射函数是唯一一种既凹又凸的函数
二次函数：设函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ 为 $f(x)=\\frac{1}{2}x^{T}A x+b^{T}x+c$ ，其中 $A \\in \\mathbb{S}^{n}$ ， $b\\in \\mathbb R^n$ ， $c\\in \\mathbb R$ 。根据上文提及的二次函数的 $Hessian$ 矩阵知 $\ abla_{x}^{2}x^{T}A x=A$ ，因此由凸性的二阶条件可知，函数 $f$ 的凸性取决于矩阵 $A$ 是否为半正定的
范数：设函数 $f : \\mathbb{R}^{n}\\rightarrow \\mathbb{R}$ 是 $\\mathbb R^n$ 上的范数，根据三角不等式以及范数的齐次性，对于任何 $x,y\\in \\mathbb R^n$ ， $0<\ heta<1$ ，有 $f(\ heta x+(1-\ heta) y) \\leq f(\ heta x)+f((1-\ heta) y)=\ heta f(x)+(1-\ heta) f(y)\\\\$ 注意，此处函数的凸性无法利用凸性的一阶条件以及二阶条件进行证明，因为范数本身可能并不是处处可微的
凸函数的非负加权和：设函数 $f_{1}, f_{2}, \\ldots, f_{k}$ 为凸函数， $w_{1}, w_{2}, \\ldots, w_{k}$ 为非负实数，设函数 $f(x)$ 为 $f(x)=\\sum_{i=1}^{k}w_{i}f_{i}(x)\\\\$ 则函数 $f(x)$ 是凸函数，因为 $\\begin{aligned}f(\ heta x+(1-\ heta) y) &=\\sum_{i=1}^{k}w_{i}f_{i}(\ heta x+(1-\ heta) y) \\\\ & \\leq \\sum_{i=1}^{k}w_{i}\\left(\ heta f_{i}(x)+(1-\ heta) f_{i}(y)\\right) \\\\ &=\ heta \\sum_{i=1}^{k}w_{i}f_{i}(x)+(1-\ heta) \\sum_{i=1}^{k}w_{i}f_{i}(y) \\\\ &=\ heta f(x)+(1-\ heta) f(x) \\end{aligned}\\\\$

在对凸函数以及凸集有了充分的认知以后，是时候来对凸优化问题进行定义了。凸优化问题有着如下形式： $\\begin{array}{cl}{\\operatorname{minimize}}&{f(x)}\\\\{\ ext{ subject to }}&{x \\in C}\\end{array}\\\\$ 即函数的输入 $x$ 服从约束集合 $C$ ，而问题的目标为最小化 $f(x)$ 。此处函数 $f$ 为凸函数，集合 $C$ 为凸集， $x$ 为优化变量。这种写法稍显不够清晰，因此将上述形式进行重写： $\\begin{array}{cl}{\\operatorname{minimize}}&{f(x)}\\\\{\ ext{ subject to }}&{g_{i}(x) \\leq 0, \\quad i=1, \\ldots, m}\\\\{}&{h_{i}(x)=0, \\quad i=1, \\ldots, p}\\end{array}\\\\$ 此处函数 $f$ 为凸函数，函数 $g_i$ 为凸函数，函数 $h_i$ 为仿射函数， $x$ 为优化变量。值得注意的是此处的不等式中不等号的方向。函数 $g_i$ 必须小于等于零，这是因为凸函数 $g_i$ 的 $0-sublevel$ $set$ 是一个凸集，这样才能保证当所有不等式约束同时成立时，约束下的可行区域依然是凸集（凸集的交集依然是凸集）。此外，此处的等式一定且只能是仿射函数，直觉上来说，等式 $h_{i}(x)=0$ 等价于两个不等式 $h_{i}(x)\\leq0$ 与 $h_{i}(x)\\geq0$ ，进一步推导知其等价于不等式 $h_{i}(x)\\leq0$ 与 $- h_{i}(x)\\leq0$ 。此时，拆解后的等式约束就可以全部归纳到前面的不等式约束 $g_{i}(x) \\leq 0$ 中，按照不等式约束的条件，所有函数 $g_i$ 都是凸函数，所以函数 $h_i,-h_i$ 都是凸函数，即函数 $h_i$ 既凸又凹，而唯一一类又凸又凹的函数就是仿射函数，所以 $h_{i}(x)$ 一定且只能是仿射函数。

有了凸优化问题的定义之后，就能对局部最优点以及全局最优点进行定义了。

局部最优点的定义：如果一个点 $x$ 服从优化问题的约束，且对于所有服从优化问题约束的点 $z$ ，都存在某个 $R>0$ 使所有服从约束 $\\|x-z\\|_{2}\\leq R$ 的点 $x,z$ 满足 $f(x)\\leq f(z)$ ，那么点 $x$ 可以被称为局部最优点。

全局最优点的定义：如果一个点 $x$ 服从优化问题的约束，且对于所有服从优化问题约束的点 $z$ 都存在 $f(x)\\leq f(z)$ ，那么 $x$ 可以被称为全局最优点。

凸优化问题的关键在于，凸优化问题中的所有局部最优点都是全局最优的。可以利用反证法对其这一点进行证明。假设点 $x$ 是凸优化问题中的一个局部最优点而非全局最优点，那么一定存在另一个服从优化问题约束的点 $y$ 使 $f(x)>f(y)$ 。根据局部最优点的定义，不存在能使约束 $\\|x-z\\|_{2}\\leq R$ 与 $f(z)<f(x)$ 同时成立且服从优化问题约束的点 $z$ 。但假设通过选择 $z=\ heta y+(1-\ heta) x\\\\$ 并选择 $\ heta=\\frac{R}{2\\|x-y\\|_{2}}$ ，那么有： $\\begin{aligned}\\|x-z\\|_{2}&=\\left\\|x-\\left(\\frac{R}{2\\|x-y\\|_{2}}y+\\left(1-\\frac{R}{2\\|x-y\\|_{2}}\\right) x\\right)\\right\\|_{2}\\\\ &=\\left\\|\\frac{R}{2\\|x-y\\|_{2}}(x-y)\\right\\|_{2}\\\\ &=R / 2 \\leq R \\end{aligned}\\\\$ 并且 $\\begin{align}f(z)&=f(\ heta y+(1-\ heta) x)\\\\ &\\leq\ heta f(y)+(1-\ heta) f(x)\\\\ &<\ heta f(x)+(1-\ heta) f(x)\\\\ &=f(x)\\\\ \\end{align}\\\\$ 即 $f(z)<f(x)$ ，而这与局部最优的定义相悖。所以点 $x$ 一定是全局最优点。

上一篇：万兴科技发布万兴播爆直播版无需设备场地随时开播

下一篇：Mysql优化的作用

新闻中心

公司新闻

APP下载 CONTACT US

APP下载

CONTACT US